Mastering the Basics of Full Adder Logic

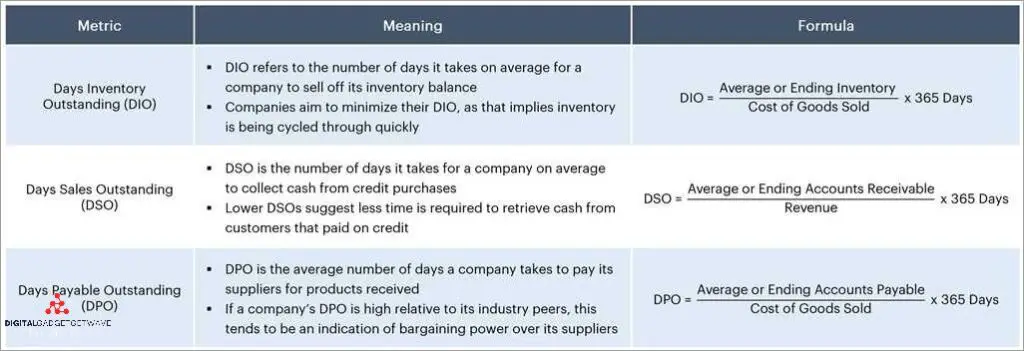
The full adder is an important component in electronics and digital circuit design. It is a combinational logic circuit that performs the addition operation on three binary inputs: two input bits and a carry bit. The output of the full adder consists of two parts: the sum bit, which represents the result of the addition operation, and the carry bit, which indicates if there is an overflow from the addition.

The full adder can be implemented using various logic gates, such as AND, OR, and XOR gates, and it can also be realized using electronic components like transistors. The circuit design of a full adder is crucial in many hardware applications, such as in computers and sequential logic circuits.

The operation of a full adder is based on binary addition rules. Each input bit is added together with the carry bit, and the result is calculated for the sum bit and the carry bit. The sum bit represents the actual addition result, while the carry bit indicates whether an overflow has occurred during the addition. The full adder can handle the addition of two binary digits and propagate the carry from a previous stage.

Overview of Full Adder Logic

A full adder is a combinational circuit that adds two bits and a carry to produce a sum and an additional carry bit. It is an essential component in the design of digital electronics, such as computers and calculators.

The full adder performs the addition operation in two stages. The first stage is the carry-in and XOR operation, where the carry resulting from the previous bit addition is combined with the current input bits using XOR gates. The second stage is the sum and carry-out operation, where the XOR gate output is combined with the carry-in bit using more XOR and AND gates to produce the sum and carry-out bits.

The full adder circuit can be implemented using boolean logic gates, such as XOR, AND, and OR gates. Each gate represents a specific boolean function, such as addition or multiplication. The transistor is the primary hardware component used to implement these boolean gates in electronic circuits.

Full adders can be used in both sequential and combinational logic circuits. In sequential circuits, multiple full adders are connected together to perform operations on multiple bits, allowing for the addition of larger numbers. In combinational logic circuits, the full adder is used as a building block to design more complex circuits.

The output of a full adder includes two bits: the sum and the carry-out. The sum represents the result of the addition operation, while the carry-out indicates whether an additional carry needs to be propagated to the next bit. These outputs can be used as inputs for subsequent full adders or other logic gates in a larger circuit.

Overall, the full adder is a fundamental component in digital electronics design, enabling the addition of binary numbers and other arithmetic operations. Its implementation using boolean logic gates and transistors allows for efficient and reliable computation in electronic devices.

Definition of Full Adder

A Full Adder is a combinational logic circuit in electronics, specifically in computer hardware design, used to perform the arithmetic operation of adding two binary numbers together. It is an essential component in many sequential circuits and is commonly used in computer processors and arithmetic logic units.

The Full Adder consists of multiple logic gates, such as transistors, that are interconnected to perform the necessary boolean functions to add two bits. It takes three input bits: two bits to be added (A and B) and a carry input (Cin) from the previous adder. The Full Adder generates two output bits: a sum output (Sum) and a carry output (Cout).

The operation of the Full Adder can be represented by a truth table, which shows the output values for all possible combinations of input bits. The logic gates inside the Full Adder circuit implement the boolean functions required to generate the correct sum and carry outputs based on the input bits.

The Full Adder is a critical component in digital electronics as it allows for efficient addition of binary numbers. By cascading multiple Full Adders together, larger binary numbers can be added together. The carry output from one Full Adder is connected to the carry input of the next Full Adder, enabling the addition of multiple bits in a sequential manner.

In summary, the Full Adder is a hardware implementation of the addition operation in binary arithmetic. It takes in two input bits and a carry input, and produces a sum output bit and a carry output bit. The Full Adder circuit is essential in computer hardware design and is widely used in various applications that require binary addition and arithmetic operations.

Importance of Full Adder in Digital Electronics

The full adder is an essential component in digital electronics. It plays a crucial role in adding two single-bit binary numbers and producing the sum and carry outputs. The hardware design of a full adder is based on transistor-level circuit implementation, making it a fundamental building block of many complex digital systems.

In a full adder, the operation is based on the principles of Boolean logic. The adder takes three inputs: the two bits to be added, and an input carry from the previous stage. It generates two outputs: the sum of the two bits and a carry out. These outputs are obtained through a combinational logic circuit that performs the addition function.

Without the full adder, the arithmetic operations performed by computers and other digital devices would not be possible. It is an essential component in the design of arithmetic and logic units (ALUs) that carry out arithmetic calculations in processors. The full adder enables the addition of multiple bits, allowing for the processing of numbers and the execution of mathematical operations.

Moreover, the sequential implementation of the full adder is crucial in the design of counters and other sequential circuits. By using multiple full adders connected in cascade, it is possible to perform addition on larger numbers with a carry bit. This sequential nature of the full adder enables the handling of numbers beyond a single bit, making it a versatile and indispensable component in digital electronics.

In conclusion, the full adder is of utmost importance in digital electronics. Its hardware design, based on transistors and combinational logic, allows for the efficient and accurate addition of binary numbers. Whether it is in the realm of computer processors or other digital systems, the full adder plays a vital role in enabling arithmetic operations and the processing of numbers in a digital environment.

Key Components of a Full Adder

A full adder is a crucial component in the field of electronics, especially in the design and implementation of digital logic circuits. It is used to perform addition operations on binary numbers, allowing for efficient computation within a computer or any other digital hardware.

The key components of a full adder include the carry-in, sum, and carry-out. These components are vital in carrying out the addition operation on two binary digits, also known as bits.

In a full adder, the carry-in input carries the carry value from the previous bit, allowing for the addition of multiple bits in a sequential manner. The output from the addition operation is represented by the sum, which is also a binary digit. The carry-out output provides the carry value to the next bit, completing the full adder circuit.

The implementation of a full adder is typically achieved through the use of boolean logic gates, such as AND, OR, and XOR gates. These gates utilize the properties of boolean algebra to perform the necessary calculations for addition.

Each component of the full adder is composed of transistors, which are fundamental building blocks in electronics. These transistors act as switches, controlling the flow of electrical signals within the circuit.

By combining multiple full adders, it is possible to create an adder circuit capable of performing addition on multi-bit binary numbers. This circuit is a key element in computer architecture as it facilitates arithmetic operations such as addition within the processor.

In summary, a full adder is an essential component in electronics and computer systems. Its key components include the carry-in, sum, and carry-out, which enable the addition of binary digits. The use of boolean logic gates and transistors allows for the efficient implementation of this crucial circuit.

Half Adder

A half adder is a logic circuit that can perform the addition of two bits. It is a fundamental building block of computer hardware and is used in the implementation of more complex circuits such as full adders.

The main function of a half adder is to generate the sum and carry bits for the addition of two input bits. It consists of two inputs, A and B, and two outputs, the sum (S) and the carry (C).

The half adder circuit can be implemented using basic logic gates such as AND and XOR gates. The XOR gate is used to generate the sum bit, while the AND gate is used to generate the carry bit.

The half adder operates on two input bits and performs a simple boolean operation to produce the sum and carry bits. It does not take into account any previous carry bits, making it a combinational circuit.

In terms of hardware, a half adder can be implemented using various electronic components, such as transistors. The design of the circuit involves arranging these components in a way that allows for the sequential operation of the gates.

The half adder is an essential component in digital electronics and computer systems. It allows for the addition of two bits, which is a fundamental operation in binary arithmetic. By combining multiple half adders, more complex operations, such as the addition of multi-bit numbers, can be achieved.

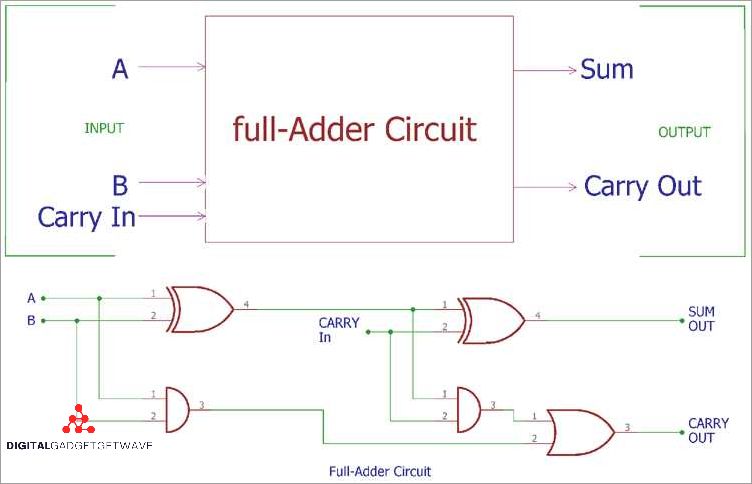
Full Adder Circuit

A full adder is a combinatorial digital circuit that is widely used in computer design and implementation. It is used to perform addition of two binary numbers represented by bits. The main function of a full adder is to add the two input bits and produce the corresponding sum and carry output bits.

The full adder circuit is composed of multiple logic gates, such as AND, OR, and XOR gates, which are interconnected to perform the addition operation. The circuit has three inputs: two input bits (A and B) and a carry-in input (CIN). It also has two outputs: a sum output (SUM) and a carry-out output (COUT).

The operation of the full adder circuit can be described using boolean logic. The SUM output is obtained by performing an exclusive OR operation (XOR gate) on the input bits A, B, and the carry-in input CIN. The COUT output is obtained by performing an OR operation (OR gate) on the input bits A, B, and the carry-in input CIN, as well as an AND operation (AND gate) on the input bits A and B.

The implementation of the full adder circuit can be done using various digital electronics components. One commonly used implementation is by using transistors, which act as switches to control the flow of current. By connecting multiple transistors in a specific configuration, the desired logic gates can be formed. These gates are then interconnected to create the full adder circuit.

The full adder circuit is an essential component in sequential and combinational logic circuits. In sequential circuits, it is used to perform addition in multi-bit addition operations. In the field of computer architecture, full adders are used in the design of arithmetic logic units (ALUs) and central processing units (CPUs) to perform arithmetic operations in computers.

Truth Table

A truth table is a logical representation of the possible outcomes of a logical operation. In the context of full adder logic, the truth table shows the relationship between the inputs and outputs of the adder function.

The full adder is a combinational logic circuit used in electronics and digital hardware designs to implement the addition of two bits, along with a carry-in bit. It is a sequential circuit that adds three input bits and produces two output bits: a sum bit and a carry bit.

The truth table for a full adder consists of eight rows, corresponding to all possible combinations of the three input bits: A, B, and the carry-in bit, C_in. Each row shows the input values and the resulting output values of the sum bit, S, and the carry-out bit, C_out.

Since the full adder is based on boolean logic, each row in the truth table represents a unique boolean operation. The inputs and outputs in the truth table can be represented by binary values (0 or 1), indicating whether the input or output is true or false.

The truth table for a full adder provides a concise representation of the adder’s behavior and allows designers to understand the circuit’s functionality. It is a valuable tool for analyzing and designing complex digital circuits using logic gates and transistors.

Applications of Full Adder Logic

The full adder logic, which is a combinational circuit that adds three binary digits together, has a wide range of applications in the field of electronics and digital hardware design. It is a fundamental building block for the operation of computers and many other digital systems.

One of the main applications of full adder logic is in arithmetic operations. By using multiple full adders, it is possible to perform addition of multi-bit numbers. The full adder circuit can be cascaded to create a larger adder, which can handle numbers with more bits. This is essential for performing mathematical operations in computers, calculators, and other digital devices.

Another important application of full adder logic is in the implementation of boolean functions. Since the basic operation of a full adder involves boolean logic, it can be used to implement complex boolean functions. By combining multiple full adders and utilizing their carry outputs, it is possible to design circuits that perform various logical operations, such as AND, OR, XOR, and NOT.

The full adder logic is also used in the design of memory circuits. Memory circuits store and retrieve data in digital systems. By using a combination of full adders and other logic gates, memory circuits can be implemented. These circuits are essential components in computer systems, storing and processing data in binary format.

In addition to the above applications, full adder logic can be used in various other fields, such as error detection and correction, digital signal processing, and communications. The ability of the full adder circuit to process binary digits and perform logical operations makes it a versatile and indispensable component in modern electronics.

Binary Arithmetic

Binary arithmetic is an essential concept in digital electronics and computer science. It involves performing mathematical operations on binary numbers, which are numbers expressed in a base-2 system using only two digits, 0 and 1.

Combinational circuits are commonly used to perform binary arithmetic operations such as addition, subtraction, multiplication, and division. One of the fundamental binary arithmetic operations is addition, which involves adding two binary numbers to produce their sum.

A full adder is a specific design of a combinational circuit used to perform binary addition. It takes in three inputs: two binary digits to be added and a carry-in bit from a previous stage of addition. The output of a full adder consists of two bits: the sum bit and the carry-out bit.

The logic function of a full adder can be implemented using electronic components such as transistors. These components are used to construct the logic gates, which are the building blocks of digital circuits. By connecting multiple full adders together, we can create an n-bit adder capable of adding two n-bit binary numbers.

In computer hardware, binary arithmetic is an essential operation performed by the central processing unit (CPU). It allows the CPU to perform calculations and manipulate data stored in binary form. This is crucial for the functioning of computer systems, as all information is ultimately represented and processed as binary data.

Binary arithmetic is based on the principles of boolean logic, which involves the use of logical operators such as AND, OR, and NOT. By applying these operators to binary digits (bits), we can perform various arithmetic operations.

Sequential circuits, which include sequential adders, are another type of circuit used for binary arithmetic. Unlike combinational circuits, sequential circuits have memory elements that allow them to store and retrieve data. This makes them suitable for performing arithmetic operations on multi-digit numbers.

In summary, binary arithmetic is a fundamental concept in digital electronics and computer science. It involves performing mathematical operations on binary numbers using combinational or sequential circuits. By understanding binary arithmetic, we can design and implement hardware to perform calculations and manipulate binary data efficiently.

Parallel Data Processing

In digital electronics, parallel data processing refers to the simultaneous processing of multiple bits of data. It is an essential function in the operation of computers and other digital systems.

The design of parallel data processing circuits involves the use of various hardware components such as adders, circuits, gates, and transistors. One of the key components is the full adder, which is a combinational circuit used to perform the addition operation on two bits of data.

Parallel data processing relies on boolean logic to perform various operations on binary data. The logic gates, such as AND, OR, and XOR, are used to manipulate and process the data in parallel.

One important concept in parallel data processing is the carry bit. When adding multiple bits together, there may be a carry from one bit to the next. The carry bit is used to propagate the carry from one stage to the next in the adder circuit.

Parallel data processing allows for efficient and fast computation of data. It is used in many applications, including image and video processing, data compression, and cryptography. Sequential data processing, on the other hand, processes data one bit at a time and is generally slower compared to parallel processing.

In summary, parallel data processing is a fundamental concept in digital electronics. It involves the simultaneous processing of multiple bits of data using combinational circuits and boolean logic. This approach allows for efficient and fast computation of data in computer systems and other digital devices.

Implementation and Design Considerations

The implementation of a full adder logic circuit involves the use of digital gates to perform various boolean operations. The full adder is a combinational circuit that adds three input bits and produces a two-bit sum and a carry output. It is an essential component in computer hardware and electronics, as it allows for sequential addition of multiple bits.

When designing a full adder, several considerations must be taken into account. One important factor is the choice of logic gates. The most commonly used gates are AND, OR, and XOR gates, which can be implemented using transistors. These gates are used to perform the necessary boolean operations to calculate the sum and carry outputs.

The design of a full adder also involves deciding on the number of bits to be added. Typically, a full adder operates on single-bit inputs and produces a two-bit sum output and a carry output. However, it is possible to design a full adder with a greater number of input bits, depending on the specific application requirements.

Another important consideration in the design of a full adder is the choice of implementation strategy. Full adders can be implemented using various techniques, such as single-bit, multiple-bit, parallel, or serial implementations. Each technique has its advantages and disadvantages, and the choice depends on factors such as speed, area, and power requirements.

In summary, the design and implementation of a full adder logic circuit require careful consideration of factors such as the choice of logic gates, the number of bits to be added, and the implementation strategy. By making informed decisions in these areas, engineers and designers can create efficient and reliable full adder circuits for use in various digital applications.

Logic Gates and Circuit Diagram

A logic gate is a basic building block of digital electronics. It is a device that performs a specific boolean function, such as AND, OR, or NOT, based on the input signals it receives. Logic gates are implemented using transistors, which are the fundamental components of digital circuits.

The circuit diagram of a logic gate shows the connections and operation of the gate. It consists of input and output lines, as well as logic gates and other components. The inputs to the gate are represented by binary signals, either 0 or 1, while the output is the result of the logic operation performed by the gate.

Logic gates are used in the design and implementation of various digital systems, including adders. An adder is a combinational circuit that can perform arithmetic operations, such as addition. A full adder is a type of adder that can add three binary digits: two input bits and a carry bit. It outputs a sum bit and a carry bit.

The circuit diagram of a full adder consists of logic gates, including AND, OR, and XOR gates, as well as other components. The input lines represent the binary digits to be added, while the output lines represent the sum and carry bits. The logic gates perform the necessary boolean operations to calculate the sum and carry.

Logic gates and circuit diagrams are essential components of computer hardware and electronics. They enable the implementation of various digital functions and operations, both combinational and sequential. By combining different logic gates, complex digital systems can be designed and built, allowing for the processing and manipulation of binary data.

Designing a Full Adder Circuit

A full adder circuit is a combinational circuit that can perform addition of two binary numbers. It is a fundamental component in digital electronics and computer systems. The main purpose of a full adder is to add two bits and a carry bit to produce a sum bit and a carry output. This circuit is implemented using transistors and other electronic components.

The full adder circuit consists of three inputs: A, B, and C (carry), and two outputs: sum and carry. It can perform the addition operation on two bits. The sum output represents the binary value of the addition, while the carry output indicates whether there is a carry generated from the addition. The functionality of a full adder is based on the boolean logic and gate operation.

To design a full adder circuit, a combination of basic logic gates such as AND, OR, and XOR gates can be used. These gates are used to manipulate the inputs and generate the desired output based on the boolean functions of addition and carry generation. The implementation of a full adder can be done using a combination of these gates in a sequential manner.

The design of a full adder circuit involves the arrangement of these gates and their interconnections to form the desired logic function. The use of transistors and other hardware components ensures the proper functioning of the circuit. The efficiency and reliability of the full adder circuit are crucial factors in its design, as it is widely used in computer systems and other digital electronics.

In conclusion, designing a full adder circuit involves the arrangement and implementation of basic logic gates to perform the addition operation. The combinational nature of the circuit, along with the sequential arrangement of gates, allows for the generation of the sum and carry outputs. This circuit plays a crucial role in digital electronics and computer systems, providing the ability to perform binary addition. The design and implementation of full adder circuits require a deep understanding of boolean logic, digital electronics, and computer architecture.

Carry Lookahead Adder

A carry lookahead adder is a type of digital circuit used in computer hardware to add two binary numbers. It is an implementation of the full adder logic, which is a combinational logic circuit that adds three binary digits: two input bits (‘A’ and ‘B’) and an input carry (‘Cin’). The output of the full adder logic is a sum bit (‘S’) and a carry bit (‘Cout’).

In a carry lookahead adder, the carry bit is generated by a separate circuit known as the carry lookahead generator. This circuit calculates the carry bits for each bit position in parallel, based on the inputs (‘A’ and ‘B’) and the input carry (‘Cin’).

The carry lookahead adder is designed to perform addition quickly by minimizing the propagation delay of the carry signal. It achieves this by using a combination of boolean logic and sequential circuit elements, such as flip-flops and transistors, to compute the sum and carry bits.

The implementation of a carry lookahead adder typically involves the use of logic gates, such as AND, OR, and XOR gates, to perform boolean operations on the input bits and generate the sum and carry bits. These gates are connected in a specific configuration to form a circuit that can perform addition.

Overall, the carry lookahead adder is an important component in the field of electronics and digital circuit design. It plays a crucial role in performing arithmetic operations in computer systems and other digital devices.