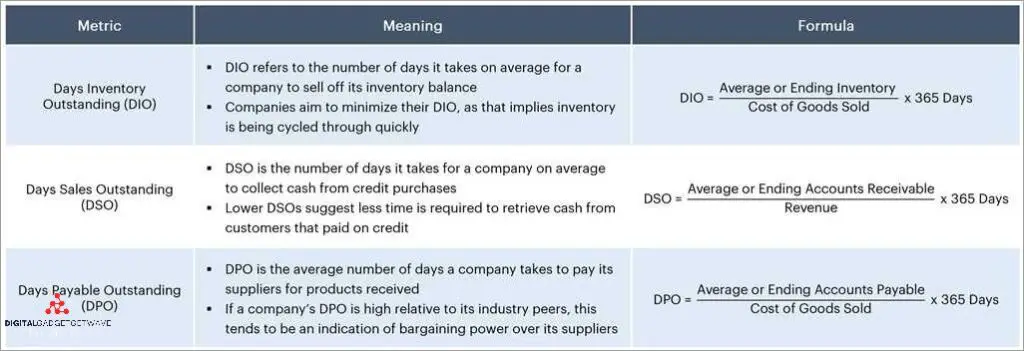
Half adder and full adder are two fundamental digital components used in arithmetic and logic calculations in binary systems. Both the half adder and full adder are combinational logic circuits that perform addition on two binary bits. However, they differ in their ability to handle carry operations and the number of bits they can add.
A half adder is a simple electronic circuit that adds two binary bits and produces a sum bit and a carry bit. It consists of two input bits, designated as A and B, and two output bits, the sum (S) and the carry (C) bit. The half adder does not consider any carry input from previous stages and can only handle addition of one bit at a time. It does not account for the possibility of a carry overflow.
On the other hand, a full adder is a more complex circuit that can add three binary bits – two input bits and a carry-in bit from a previous stage. In addition to producing a sum bit and a carry-out bit, it also takes into account the carry input, allowing for the addition of multiple bits. This makes the full adder suitable for more complex arithmetic calculations and handling possible carry overflow.
Both the half adder and full adder are crucial components in the design of digital circuits and computer systems, as they form the building blocks for performing arithmetic operations. They are based on boolean algebra and employ logic gates to carry out addition. The outputs of these circuits are used in further calculations or fed into other components of a larger system.
In summary, the half adder and full adder are essential components in digital electronics and perform binary addition. While the half adder adds two bits without considering any carry, the full adder handles three bits, including a carry input from previous stages. Understanding the difference between these two adders is crucial in designing efficient and accurate circuits for arithmetic and logic operations.
Contents
- 1 What is a Half Adder?
- 2 What is a Full Adder?
- 3 Comparison
- 4 Differences
- 5 Similarities
- 6 Applications
- 7 Half Adder Applications
- 8 Full Adder Applications
- 9 FAQ about topic “Understanding the Difference Between Half Adder and Full Adder”
- 10 What is the difference between a half adder and a full adder?
- 11 Can a half adder be used to add three binary digits?
- 12 What is the purpose of a carry in a full adder?
- 13 What are the inputs and outputs of a full adder?
- 14 Is there any advantage of using a full adder over a half adder?
What is a Half Adder?
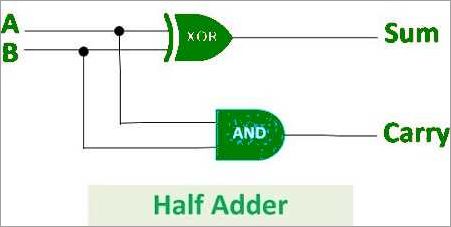
A half adder is a component in boolean logic that is used for the implementation of binary addition. It is a digital circuit designed to perform the binary SUM and CARRY calculation of two input bits. The half adder consists of two inputs, A and B, and two outputs, SUM and CARRY.
The half adder uses logic gates to perform the binary addition of the input bits. The SUM output represents the result of the addition without considering any carry from previous bits, while the CARRY output represents any carry that occurs during the addition.
The half adder circuit can be represented using logic gates such as AND, XOR, and OR gates to perform the binary addition. The XOR gate is used to calculate the SUM output, while the AND gate is used to calculate the CARRY output.
The half adder is a combinational circuit, as it performs the addition calculation without any memory or state. It is a basic building block for more complex arithmetic operations in digital circuits, such as the full adder.
In binary arithmetic, the half adder is used to add two bits together. The input bits can be either 0 or 1, and the output bits can also be either 0 or 1. If the addition of the two input bits results in a sum of 2 (binary 10), it causes an overflow, and the CARRY output will be 1.
Definition
An adder is an essential component in electronics and digital logic design used for the implementation of arithmetic calculations. It is a circuit that performs the addition of two binary numbers, known as bits, and produces the sum and carry outputs.
A half adder is a basic adder circuit that can only add two single-digit binary numbers and produce a sum and carry output. It does not consider any carry produced from previous addition operations, which can result in an overflow in some cases.
On the other hand, a full adder is a more advanced adder circuit that can add three single-digit binary numbers – two input bits and the carry from the previous addition operation. It considers all possible combinations of inputs and generates both the sum and carry outputs, taking into account any carry from previous addition operations.
The main difference between a half adder and a full adder is the consideration of the carry input. While a half adder can only handle single-digit addition, a full adder can handle multi-digit addition and can effectively add more complex binary numbers.
In terms of implementation, both half adders and full adders are built using boolean logic gates, such as AND, OR, and XOR gates. These gates are combined in specific ways to create the desired adder circuit.
In summary, a half adder is a basic digital circuit that performs single-digit addition, while a full adder is a more advanced circuit that can handle multi-digit addition. The design and implementation of these adders involve using boolean logic gates to produce the necessary outputs, including the sum and carry. When working with binary numbers and arithmetic calculations, understanding the difference between half adders and full adders is essential for designing efficient and accurate digital circuits.
Logic Diagram
The logic diagram is a graphical representation of the digital circuit that implements the half adder or full adder. It consists of various combinational logic gates, such as AND, OR, and XOR gates, connected together to perform the required arithmetic calculation.
In a half adder logic diagram, there are two inputs, usually referred to as A and B, which are the binary bits to be added. The logic diagram also includes two outputs, which are the sum (S) and the carry (C). The half adder circuit is designed to calculate the sum of the two input bits and produce a carry, if necessary, for further addition.
On the other hand, a full adder logic diagram includes three inputs: A, B, and an input carry (Cin), which is the carry generated from the previous bit addition. The full adder produces both the sum (S) and the carry (Cout) outputs. It is used in multi-bit binary addition, where the carry generated from each bit addition is propagated to the next bit.
The design of the logic diagram involves the use of boolean logic and the application of boolean algebra to determine the appropriate gates and their connections. The logic gates are the fundamental components of the logic diagram, representing the boolean operations that are performed on the binary inputs. The inputs and outputs of each gate are connected using wires, which carry the binary signals.
The logic diagram can be implemented using different combinations of logic gates, depending on the desired functionality and optimization requirements. The efficient implementation of the logic diagram ensures proper handling of overflow conditions and accurate calculation of the binary arithmetic.
In summary, the logic diagram is a visual representation of the circuit that performs addition in binary arithmetic. It consists of logic gates connected in a specific way to generate the sum and carry outputs. The design of the logic diagram involves the use of boolean logic and the selection of appropriate gates to achieve the desired functionality.
Truth Table
A truth table is a fundamental component of digital logic and is used to define the behavior of a digital circuit. It provides a systematic representation of all input combinations and the corresponding output values of a given logic gate or circuit.
In the context of half adders and full adders, the truth table shows the results of the addition of two binary bits and the carry generated during the addition. For a half adder, which is a basic component of an adder circuit, the truth table will have two input bits (A and B) and two output bits (Sum and Carry).
| A | B | Sum | Carry |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
The truth table for a full adder, which is an adder circuit capable of handling carry inputs and outputs, will have three input bits (A, B, and Carry-in) and two output bits (Sum and Carry-out).
| A | B | Carry-in | Sum | Carry-out |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
The truth tables allow us to understand the logic behind the adders and design efficient and reliable digital circuits for arithmetic calculations in electronics.
What is a Full Adder?
A full adder is a component in boolean arithmetic that is used for the calculation of binary numbers. It is an important part of the design and implementation of digital electronics.
A full adder is a logic circuit that takes in three input bits – A, B, and carry-in – and produces two output bits – sum and carry-out. The carry-in represents the carry from the previous bit addition, while the carry-out represents the carry to the next bit addition. The sum is the result of the addition of the three input bits.
One of the main advantages of a full adder over a half adder is its ability to handle overflow, which occurs when the sum of two binary numbers is greater than the maximum value that can be represented by the number of bits available. The full adder includes an additional input and output to handle carry, ensuring accurate calculations even with large numbers.
A full adder is typically implemented using logic gates, such as AND, OR, and XOR gates, which perform basic boolean operations. These gates are interconnected in a specific way to create the desired logic implementation for the adder. The carry-out and sum outputs are generated by these interconnected gates based on the input bits.
The full adder is a fundamental building block in many digital circuits and is commonly used in various applications, including arithmetic operations in processors, memory devices, and communication systems. Its ability to perform binary addition accurately and handle overflow makes it a crucial component in the field of digital electronics.
Definition
In the field of digital electronics and boolean logic, an adder is a circuit component used for the arithmetic calculation of binary numbers. It is capable of performing addition of two binary numbers and can be implemented as a full adder or a half adder.
A half adder is a basic adder circuit that can add two single binary digits, also known as bits. It consists of two inputs, A and B, which represent the binary digits to be added, and two outputs, sum (S) and carry (C). The sum output represents the least significant bit of the addition result, and the carry output represents the carry bit that is generated when the addition exceeds the capacity of a single bit.
A full adder, on the other hand, is a more complex adder circuit that can add three single binary digits – two input bits and a carry bit. In addition to the inputs and outputs of a half adder, a full adder has an additional input, carry-in (Cin), which represents the carry bit from the previous less significant bit addition. The full adder performs the addition of the three bits and generates two outputs – sum (S) and carry-out (Cout). The sum output represents the least significant bit of the addition result, and the carry-out represents the carry bit that is generated when the addition exceeds the capacity of a single bit.
Adders are an essential component in the design of digital circuits and are used in various arithmetic and logical operations. They are commonly used in processors, calculators, and other electronic devices that perform calculations. The implementation of adders can vary depending on the specific requirements of the circuit or system, but they are typically built using boolean logic gates such as AND, OR, and XOR gates.
Logic Diagram
In electronics, a logic diagram is a graphical representation of a binary logic circuit. It shows the flow of electrical current through various components such as gates, which are used to implement logical operations.
A logic diagram for a half adder, which is a basic building block of arithmetic circuits, consists of two inputs (A and B) and two outputs (SUM and CARRY). These outputs represent the binary sum and carry of the input bits. The logic diagram includes logic gates like AND and XOR, which perform Boolean calculations to determine the values of SUM and CARRY.
A full adder, on the other hand, is a more complex component that can add three binary digits: the two input bits and an input carry. Its logic diagram includes multiple logic gates and additional inputs and outputs to handle the carry operation. The full adder is used in digital arithmetic circuits to perform addition of multiple bits.
One important aspect of logic diagrams is their combinational nature. This means that the output values of the circuit depend solely on the current input values, without any memory or feedback. Combinational logic circuits are used for fast and efficient calculation of logic operations.
Logic diagrams are essential in the design and implementation of digital circuits, as they provide a visual representation of the circuit’s structure and logic. They help engineers and designers understand how different components are connected and how they interact to perform specific operations. Logic diagrams are also useful for troubleshooting and testing circuits, as they can help identify potential errors or problems in the design.
Truth Table
Truth table is a useful tool in electronics and digital logic design. It is a table that displays all possible combinations of inputs and corresponding outputs of a logical or combinational circuit.
In the context of half adder and full adder, the truth table represents the inputs and outputs of these arithmetic circuits. Both half adder and full adder are used in digital electronics to perform binary addition.
In the truth table of a half adder, there are two input bits: A and B. The output sum indicates the result of the binary addition of A and B. The output carry represents any carry that occurs during the addition operation.
A full adder, on the other hand, has three input bits: A, B, and carry-in. The output sum still represents the result of the binary addition, while the output carry is used as carry-out to the next bit.
The truth table for a full adder is more complex than that of a half adder because it takes into account the carry-in from the previous bit. The carry-out is important in a full adder because it allows for the calculation of multi-bit additions without overflow.
The truth table is a fundamental tool in the design and implementation of digital circuits. It helps engineers and designers understand the behavior of logic gates and combinational circuits.
Comparison
When it comes to the topic of half adder and full adder, it is important to understand the differences between them. Both of them are used in the field of electronics for performing binary arithmetic calculations. However, there are specific variations in terms of their functionality and design.
Starting with the half adder, it is a basic electronic circuit that adds two binary digits, resulting in a sum and a carry. It has two inputs, representing the two bits to be added, and two outputs: the sum and the carry. The half adder is a combinational logic implementation that uses basic logic gates, such as AND and XOR gates, to perform the addition.
On the other hand, a full adder is an advanced version of the half adder and has an additional input, which is the carry from the previous stage. This allows the full adder to add three binary digits: two inputs and the carry input. Just like the half adder, it produces a sum and a carry output. The design of a full adder involves a more complex gate arrangement, using XOR, AND, and OR gates, to achieve the desired functionality.
One important distinction between the two is that a half adder can only add two bits at a time, while a full adder can add three bits. This makes the full adder more versatile and suitable for more complex calculations. Additionally, the carry output of a full adder can be used as the carry input for the next stage, allowing for multi-bit addition.
In terms of practical applications, half adders are often used in simpler digital circuits, where only two bits need to be added. They are commonly used in basic arithmetic operations, such as adding two binary numbers or performing boolean calculations. On the other hand, full adders are used in more complex circuits and systems, where multi-bit addition is required. They are commonly used in processors, calculators, and other advanced digital devices.
In conclusion, while both half adders and full adders are important components in digital electronics, the full adder is more versatile and capable of handling more complex calculations. The design and implementation of these circuits involve different combinations of logic gates, resulting in distinct functionality and uses.
Differences
When it comes to electronics, the combinational circuit is an essential component for various operations. One such operation is addition, which can be accomplished through the use of adders. Adders are logic gates that are designed to perform arithmetic calculations, specifically the addition of binary numbers.
There are two types of adders: half adder and full adder. The main difference between these two adders lies in their ability to handle the carry bit.
- A half adder is a basic adder that can only add two single-bit inputs and produce a sum and carry output. It does not have the capability to handle a carry input from a previous stage.
- On the other hand, a full adder is a more advanced adder that can add three single-bit inputs: two data bits and a carry bit. It produces a sum output, as well as a carry output.
The design of a half adder is relatively simple, as it only requires two boolean logic gates: an XOR gate and an AND gate. This makes it a basic building block for more complex adders and other digital circuits.
A full adder, on the other hand, requires three boolean logic gates: two XOR gates and an AND gate. This additional gate allows the full adder to handle the carry input, resulting in a more versatile and powerful adder.
The sum output produced by both the half adder and full adder represents the least significant bit of the addition calculation. However, in the case of a full adder, the carry output represents the carry bit that is propagated to the next stage of the addition calculation, allowing for the addition of multiple bits.
In summary, while both the half adder and full adder are used for binary addition in digital circuits, the full adder is more versatile and can handle carry inputs, allowing for the addition of multiple bits. This makes it a more suitable choice for complex calculations and implementations.
Number of Inputs
In the field of digital electronics and boolean logic design, adders are essential components for arithmetic calculations. An adder is a combinational circuit that can be used to perform binary addition. The number of inputs in an adder determines its ability to handle different bit sizes of numbers.
A half adder is a basic adder that can add two single-bit binary numbers. Hence, it has two inputs: one for each bit. The half adder outputs a sum bit and a carry bit, indicating if there is an overflow in the addition. It is a fundamental component in building more complex adders.
On the other hand, a full adder is a more advanced adder that can add two single-bit binary numbers and an additional carry input. This means that a full adder has three inputs: two for the bits and one for the carry. The full adder outputs a sum bit and a carry bit, allowing it to perform more complex arithmetic calculations.
When it comes to the number of inputs, the half adder can handle two inputs, while the full adder can handle three inputs. This difference in inputs enables the full adder to handle carry bits from previous calculations, making it suitable for multi-digit addition. The full adder is an essential component in building larger arithmetic circuits.
Carry Output
The carry output is an important component in both half adders and full adders in electronics. In boolean arithmetic, when performing a binary addition calculation, a carry output is generated when the sum of two input bits is greater than or equal to two. This carry output is used to add the result of the previous bit addition, ensuring that the arithmetic calculation is carried out correctly.
In a full adder, three inputs (A, B, and a carry) are used to generate two outputs: a sum and a carry. The carry output is used to propagate the carry bit from one bit addition to the next, ensuring that the arithmetic calculation can be performed for multiple-bit numbers. Without the carry output, the arithmetic calculation would be limited to only a single bit.
The carry output is also important in detecting overflow in an arithmetic calculation. If the input bits and the carry result in a sum that is larger than the maximum value that can be represented by the number of bits being used, an overflow condition occurs. The carry output allows the detection of this overflow, which is important in preventing errors in calculations.
The design and implementation of the carry output component in a full adder involve combinational logic circuits. These circuits use boolean logic gates, such as AND, XOR, and OR gates, to calculate the sum and carry outputs based on the input bits and the carry input. As a result, the carry output is a crucial element in the overall functioning of a full adder.
Overall, the carry output plays a significant role in both half adders and full adders in electronics. It is necessary for performing arithmetic calculations, detecting overflow, and ensuring the correct propagation of carry bits in multiple-bit additions. Understanding the importance and implementation of the carry output is essential in designing and working with arithmetic circuits in binary systems.
Sum Output

The sum output is an essential component of a digital circuit, especially in the field of electronics and combinational logic design. It is used in binary arithmetic and plays a crucial role in the addition of two binary numbers. The sum output is the result of the addition calculation, which is performed using the Boolean logic gates and the half and full adder implementations.
In a half adder, the sum output represents the addition of the two input bits without considering any carry from a previous calculation. It is obtained by performing an XOR operation on the input bits. If there is no carry, the sum output will be a simple addition of the individual bits. However, if there is a carry, it will not be considered in the sum output of a half adder.
On the other hand, the sum output of a full adder considers both the input bits and the carry from a previous calculation. It is obtained by performing an XOR operation on all three inputs: the two input bits and the carry input. The result will be the sum of the three inputs, taking into account any carry from previous calculations.
The sum output is an important aspect of addition in binary arithmetic. It represents the result of the addition calculation and determines the value of the corresponding bit in the final result. It can either be a 0 or a 1, depending on the input bits and any carry from previous calculations.
In summary, the sum output is a crucial component in the design and implementation of half adders and full adders. It represents the addition result and takes into account the input bits and any carry from previous calculations. With the help of logic gates and Boolean operations, the sum output allows for efficient binary arithmetic in digital circuits.
Similarities
Half adder and full adder are both components used in digital electronics and arithmetic calculations. They are both types of adders used to perform binary addition by taking two input bits and producing a sum and a carry output.
Both half adder and full adder consist of logic gates, such as AND, XOR, and OR gates, which perform arithmetic and boolean operations to generate the output. These gates are fundamental building blocks in digital electronics and are used to implement various mathematical and logical operations.
Both adders, whether half or full, work on the principle of bit-by-bit addition. They take two binary input bits and generate a sum output, which is the result of the addition of the two bits. They also generate a carry output, which represents the overflow or carry-over from the previous bit addition.
The design and implementation of both half adder and full adder involve the use of combinational circuits. These circuits are responsible for generating the sum and carry outputs based on the input bits and logic gate operations.
Binary Addition
In digital electronics, binary addition is an important concept in arithmetic and logic design. It involves the addition of two binary numbers, bit by bit, using a combination of boolean logic gates and adder circuits.
The process of binary addition starts with the calculation of the sum of the individual bits of the two binary numbers. This is done by applying the boolean logic rules of OR, AND, and XOR to each pair of corresponding bits. These logic gates are implemented using electronic circuitry, which can be represented using standard symbols.
The combinational circuit used to perform binary addition is called a binary adder. It consists of two primary components: a half adder and a full adder. A half adder is used to add two single bits, while a full adder is used to add two bits along with a carry bit received from a previous addition.
When performing binary addition, each bit is added sequentially, starting from the rightmost bit and moving towards the left. The carry bit from each addition is propagated to the next bit, ensuring that the sum is calculated correctly. If the addition of two bits and the carry bit produces a result greater than 1, an overflow occurs, indicating that the sum cannot be represented using a single bit.
The result of a binary addition is a sum and a carry. The sum represents the bits that make up the total of the addition, while the carry represents the overflow bit that is carried to the next position. It is important to consider the carry when adding multiple binary numbers to ensure accurate results.
In summary, binary addition is a fundamental operation in digital electronics and is used extensively in arithmetic and logic calculations. It involves the use of boolean logic gates and adder circuits to add binary numbers bit by bit. The concept of carry and overflow is important to consider when performing binary addition to ensure accurate results in calculations.
Boolean Expressions

In the field of digital electronics and logic design, boolean expressions are used to represent and manipulate logic states. They are a fundamental part of the implementation of arithmetic and logical operations in electronic circuits.
A boolean expression is a mathematical expression that consists of variables, logical operators, and constants. It is used to describe the logic or behavior of a component or a circuit. In the context of adders, boolean expressions are used to calculate the sum and carry outputs based on the input bits.
For a half adder, the boolean expressions for the sum and carry outputs are as follows:
sum = A XOR B
carry = A AND B
These expressions utilize the XOR and AND logical operators to perform the bitwise addition of the input bits. The sum output represents the result of the binary addition operation, while the carry output indicates if there was an overflow or a carry beyond the highest bit.
On the other hand, a full adder extends the functionality of a half adder to include a carry-in input. Its boolean expressions for the sum and carry outputs are:
sum = (A XOR B) XOR C_in
carry = (A AND B) OR ((A XOR B) AND C_in)
These expressions incorporate the XOR, AND, and OR logical operators to perform the addition of three input bits. The sum output is obtained by adding the three bits, considering the carry-in input, while the carry output accounts for any carries generated during the addition.
Overall, boolean expressions play a crucial role in the design and analysis of digital circuits. They allow for the manipulation and calculation of logic states, enabling efficient and accurate calculations in electronic systems.
Applications
The half adder and full adder are fundamental building blocks in digital electronics and are widely used in numerous applications. Their primary purpose is to perform binary addition, which is essential in various computational and cryptographic systems.
One of the key applications of half adders is in the design of digital systems that require simple binary addition. These systems often involve the calculation of sums and carries in binary numbers. Half adders are particularly useful in such cases as they can process individual bits of the binary numbers and produce the corresponding sum and carry outputs.
Full adders, on the other hand, are employed in more complex arithmetic operations that involve multi-bit addition. They are extensively used in arithmetic logic units (ALUs), which are key components in computer processors. ALUs perform various arithmetic operations, including addition, subtraction, and multiplication, and full adders play a critical role in executing these calculations.
In addition to their use in arithmetic operations, adders are also employed in the implementation of logic systems. They can be used to construct complex logic gates and circuits that perform boolean operations. By combining multiple half adders or full adders, designers can create more sophisticated digital circuits to execute complex logical operations.
Furthermore, adders are crucial in error detection and correction systems. They are used to perform bitwise addition and comparison to detect any errors that may occur during data transmission or storage. When the adder detects an overflow, it indicates that an error has occurred, enabling the system to take appropriate measures to correct or notify about the error.
Overall, half adders and full adders are essential components in the field of digital electronics and find various applications in binary arithmetic, logic design, error detection, and correction systems. Their versatility and compact design make them indispensable in many electronic devices and systems.
Half Adder Applications

A half adder is a basic arithmetic electronic circuit that performs addition of two binary digits. It is an important component in digital design and can be used in many applications where binary addition is required.
One of the main applications of a half adder is in the design of a full adder. A full adder is a more complex circuit that can add three binary digits – two input bits and a carry-in bit. The design of a full adder requires two half adders, one for the sum output and another for the carry output. The carry output from the first half adder is connected to the carry input of the second half adder, allowing for the addition of the three bits.
In addition to being used in the design of full adders, half adders can also be used in boolean logic calculations. The sum output of a half adder can be connected to other logic gates or components to perform more complex calculations. This allows for the creation of binary adders and multipliers, which are essential in digital circuit design.
Another application of a half adder is in digital overflow detection. In binary addition, a carry occurs when the sum of two binary digits is greater than the maximum value that can be represented by a single bit. By examining the carry output of a half adder, it is possible to detect overflow conditions. This can be useful in situations where it is necessary to prevent overflow and ensure accurate results in arithmetic operations.
In summary, a half adder is a fundamental component in digital circuit design that has various applications in the field of electronics. It can be used in the design of full adders, in boolean logic calculations, and in digital overflow detection. Its simplicity and efficiency make it a valuable tool in the field of digital arithmetic and computation.
Simple Arithmetic
In the field of binary arithmetic, the concept of simple arithmetic is crucial. It involves the basic operations of addition and subtraction, which are fundamental for any calculations in the digital domain. Understanding how these operations are implemented in electronic circuits is essential for designing efficient and effective systems.
One of the key components in simple arithmetic is the adder circuit, which is used to perform the addition of binary numbers. The adder circuit is a combinational logic circuit that takes two input bits (A and B) and produces two output bits: the sum (S) and the carry (C). The two input bits are the binary digits being added, while the output bits represent the result of the addition.
In a binary adder, each bit is processed individually using Boolean logic gates. The full adder is a more complex version of the half adder, as it takes into account not only the current bit being added but also the carry generated by the addition of the previous bit. This allows for the accurate calculation of the sum and carry for multi-bit additions.
Arithmetic operations using adders can be extended to any number of bits. This allows for the addition of large numbers using multiple adder circuits, making it possible to perform calculations with precision and accuracy. However, it is important to consider the limitations of the adder circuit, such as the possibility of overflow when the sum of two numbers exceeds the maximum value that can be represented by the available number of bits.
In conclusion, simple arithmetic is an essential concept in the field of electronics and digital design. It involves the use of adder circuits to perform binary addition, allowing for the accurate calculation of sums and carries. By understanding how these components work, it becomes possible to design and implement efficient systems for various applications.
Computer Processors
A computer processor is a central component of a computer system that performs logic and arithmetic operations on binary data. It is responsible for executing instructions and performing calculations to carry out various tasks.
Processors use a combination of logic circuits, electronics, and gates to process and manipulate binary data. They can perform both boolean logic operations, such as AND, OR, and NOT, and arithmetic operations, such as addition, subtraction, multiplication, and division.
One important component of a processor is the adder circuit. An adder is a combinational digital circuit that is used to perform addition of binary numbers. It takes two binary inputs, called operands, and produces a binary output, called the sum. The adder circuit also generates a carry output, which indicates if there is a carry-over from the addition of the previous bit.
There are different types of adders that can be used in processor design, including half adders and full adders. A half adder is a simple adder that adds two bits and produces a sum and a carry output. A full adder, on the other hand, can add three bits and also produces a sum and a carry output. Full adders are used in multi-bit addition to handle carry-over from previous bits.
In addition to performing arithmetic calculations, processors also handle overflow, which occurs when the result of an operation exceeds the maximum value that can be represented by a given number of bits. Processors use various techniques to detect and handle overflow, such as setting an overflow flag or wrapping the result around.
Overall, computer processors are complex electronic devices that play a crucial role in executing instructions and performing calculations in a computer system. They utilize a combination of logic circuits, adder circuits, and other components to process binary data and perform various operations.
Full Adder Applications
The Full Adder is a combinational digital logic component that is used to perform binary addition and calculate the sum and carry outputs. It is an essential component in arithmetic calculation and overflow detection in electronic devices.
One of the main applications of the Full Adder is in the design of arithmetic circuits, such as binary adders. It is used to add two binary numbers together, taking into account any carry from a previous bit. The Full Adder can be cascaded to create larger adders for multi-bit numbers.
In addition to arithmetic calculations, the Full Adder can also be used in other applications, such as in counters and memory units. It provides the necessary logic to increment or decrement the values stored in these circuits. The carry output of the Full Adder is used to propagate the carry in a multi-bit counter or to detect overflow.
The Full Adder is also used in the implementation of more complex digital systems, such as processors and microcontrollers. It plays a crucial role in performing binary addition in these systems and enabling them to carry out various arithmetic and logical operations.
Furthermore, the Full Adder can be used in gate-level design and boolean function implementation. It can be combined with other logic gates to create more complex circuits and perform a wide range of operations. Its versatile nature and ability to process multiple bits at once make it an essential component in many electronic systems.
In summary, the Full Adder has various applications in the field of electronics. It is a fundamental component in arithmetic calculations, overflow detection, counters, memory units, processors, and other digital systems. Its ability to perform binary addition and generate carry outputs makes it a crucial element in the design and implementation of many electronic circuits.
Parallel Adders
In digital logic, a parallel adder is a combinational logic circuit that is used to perform the arithmetic addition of two binary numbers. It is an important component in the design of electronic calculators, processors, and other digital systems that require fast addition operations.
A parallel adder can handle multiple bits simultaneously, which allows for faster addition compared to a serial adder. It is capable of performing addition with carry input and carry output, which helps in managing overflow during the arithmetic calculation.
One common implementation of a parallel adder is a full adder. A full adder is a binary adder that adds three binary digits: a carry-in bit, and two input bits. It outputs a sum bit and a carry-out bit. By cascading multiple full adders together, a parallel adder can be built to handle larger numbers.
A parallel adder can be designed using boolean logic gates such as AND, OR, and XOR gates. The carry output of one full adder is connected to the carry input of the next full adder, forming a chain. This allows for the propagation of the carry bit across multiple bits during addition.
Parallel adders are commonly used in various applications that require fast and efficient addition operations. They play a crucial role in computer architecture, data processing, and other fields that involve binary arithmetic. Their design and implementation are important topics in the study of digital electronics.
Arithmetic Logic Units
An Arithmetic Logic Unit (ALU) is a key component of a digital computer’s central processing unit (CPU). It is responsible for performing arithmetic and logical operations on binary numbers. The ALU is designed to handle the basic operations such as addition, subtraction, multiplication, and division.
The ALU is implemented using various combinational logic circuits, including half adders and full adders. These adders are used to perform binary addition. A half adder can add two single-bit numbers and provide a sum and a carry output. However, it cannot handle a carry input from a previous stage. In contrast, a full adder can handle carry inputs, thereby allowing for multi-bit addition.
In addition to addition and subtraction, an ALU can also perform logical operations such as AND, OR, and XOR. These operations are achieved using boolean logic gates, such as AND gates, OR gates, and XOR gates. These gates take binary inputs and produce binary outputs based on the specified operation.
One of the important considerations in ALU design is handling overflow. Overflow occurs when the result of an operation exceeds the range of representable numbers. For example, adding two positive numbers may result in a negative number, which is not representable in the given number system. ALUs employ techniques such as overflow flags or additional circuitry to detect and handle overflow conditions.
The ALU can be designed using various components, including multiplexers, multiplexor-based adders, and look-ahead carry generators. These components work together to perform complex arithmetic and logical calculations efficiently. The design of an ALU involves careful consideration of factors such as speed, power consumption, and cost.
In summary, an Arithmetic Logic Unit is a crucial component in a digital computer’s CPU that performs arithmetic and logical operations. It is implemented using combinational logic circuits, such as half adders and full adders. The ALU can handle addition, subtraction, multiplication, division, and logical operations using boolean logic gates. It also incorporates mechanisms to handle overflow conditions. The design of an ALU involves careful consideration of various factors to ensure efficient and reliable operation.
FAQ about topic “Understanding the Difference Between Half Adder and Full Adder”
What is the difference between a half adder and a full adder?
A half adder is a digital circuit that adds two single binary digits and produces a sum and a carry. It has two inputs and two outputs. A full adder, on the other hand, is a more advanced circuit that can add three binary digits and produce a sum and a carry. It has three inputs and two outputs.
Can a half adder be used to add three binary digits?
No, a half adder can only add two binary digits. If you want to add three binary digits, you will need to use a full adder.
What is the purpose of a carry in a full adder?
In a full adder, the carry input represents the carry generated from adding the previous set of binary digits. It is used to add the carry from the previous column to the current column of digits being added.
What are the inputs and outputs of a full adder?
The inputs of a full adder are three binary digits: A, B, and the carry input (Cin). The outputs of a full adder are the sum (S) and the carry output (Cout).
Is there any advantage of using a full adder over a half adder?
Yes, there are several advantages of using a full adder over a half adder. A full adder can add three binary digits, while a half adder can only add two. Additionally, a full adder has a carry input, which allows it to chain together multiple full adders to add numbers of any length. Finally, a full adder is more versatile and can be used in more complex arithmetic and logic operations.