Understanding the x-axis in math: Definition and key properties

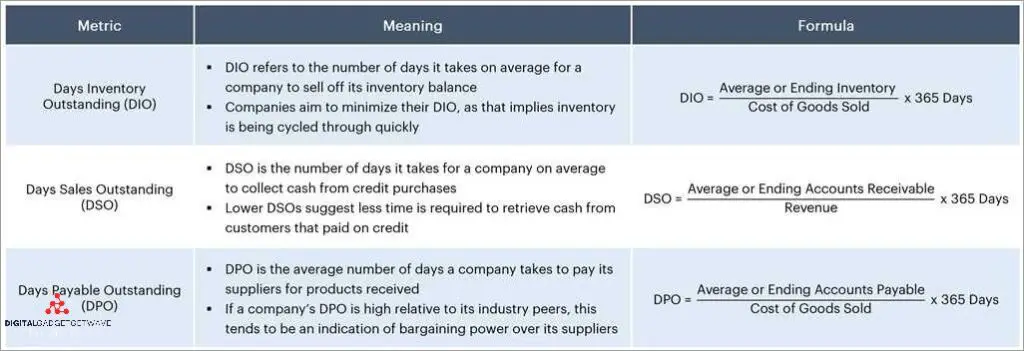
The x-axis is a fundamental concept in mathematics, particularly in the field of geometry, that plays a crucial role in representing and analyzing data. It is a horizontal line on a Cartesian plane, which is a two-dimensional space used for plotting points and graphing functions. The x-axis is also known as the horizontal axis and is used to represent the independent variable, typically denoted as ‘x’.

On the x-axis, numbers are represented in a continuous manner, with positive numbers extending to the right of the origin and negative numbers extending to the left. The origin, located at the point where the x-axis and y-axis intersect, represents the point of reference from which all other coordinates are measured. This allows for a systematic representation of data on the graph and helps in understanding the relationships between variables.

The x-axis is equipped with a scale that provides a measurement system for the entire interval covered by the graph. This allows for precise representation of the data points and assists in interpreting the graph accurately. The scale on the x-axis allows us to determine the distance between any two points on the line, helping us understand the relationships and patterns within the data.

In addition to its key properties in graphing, the x-axis also has significant implications in various mathematical concepts. In algebra, the x-axis is used to represent variables and equations, helping us solve equations and determine solutions. In geometry, the x-axis is used to represent the x-coordinate of points in a coordinate plane, allowing for a clear representation of shapes and figures.

In conclusion, the x-axis is a vital component in the field of mathematics. It provides a framework for representing data, solving equations, and analyzing relationships between variables. Understanding the key properties and importance of the x-axis is essential for mathematical proficiency and is applicable in various fields beyond math.

The Definition of the X-Axis

The x-axis is a fundamental concept in math and is an essential element in coordinate geometry. It is a horizontal line that extends infinitely in both directions in a 2-dimensional plane. The x-axis represents the horizontal axis on a Cartesian coordinate system where points are located based on their x-coordinate and y-coordinate values.

The x-axis is typically represented as a straight line that intersects with the y-axis at the origin (0,0). The origin is the point where the x-axis and y-axis meet and serves as the reference point for determining the position of other points on the coordinate plane. The x-coordinate of a point on the x-axis is always zero, as it does not change along the x-axis.

The x-axis is divided into intervals or segments, each representing a specific range of values. These intervals can be labeled or scaled, allowing for precise measurements and comparisons. The scale on the x-axis helps determine the numerical value associated with each point or interval on the x-axis.

The x-axis is used to represent independent variables in mathematical equations and functions. It is commonly used to graphically represent the relationship between two variables, with the x-axis representing the input or independent variable and the y-axis representing the output or dependent variable. By plotting points on the x-axis, we can visualize how the value of the variable changes as the independent variable changes.

Placement and Orientation

In mathematics, the x-axis is an imaginary line that is used to represent the horizontal placement and orientation of points and objects on a graph or coordinate plane. It is an essential element of Cartesian geometry, a branch of mathematics that deals with the relationship between points and the coordinate system.

The x-axis is a straight line that runs horizontally across the graph or coordinate plane. It is typically labeled with numerical values to represent different intervals or scales. The interval or scale of the x-axis determines the range of values that can be represented on the graph. Positive values are usually placed to the right of the origin, while negative values are placed to the left.

The origin is the point where the x-axis and the y-axis intersect. It serves as the reference point for determining the coordinates of other points on the graph. The x-axis and the y-axis divide the coordinate plane into four quadrants, each with its own set of coordinates. The x-axis itself is located in the center of the plane.

When graphing a variable or a function, the x-axis represents different values that the variable or function can take on. For example, in a graph representing the height of a plant over time, the x-axis could represent different time intervals, such as days or weeks. The vertical direction on the graph represents the dependent variable, while the horizontal direction represents the independent variable.

In geometry, the x-axis is often used in conjunction with the y-axis to plot points and create shapes. By specifying coordinates on the x-axis and the y-axis, it is possible to locate a point or draw geometric figures on a plane. The x-axis provides the horizontal reference for these calculations and helps determine the position of objects in relation to each other.

Coordinate System

In mathematics and geometry, a coordinate system is used to represent the position of points in a space. A coordinate system consists of a vertical and a horizontal axis that intersect at a point called the origin.

The vertical axis is also known as the y-axis, and it represents the range or values of a variable in the vertical direction. In a two-dimensional coordinate system, the vertical axis is perpendicular to the horizontal axis.

The horizontal axis is also known as the x-axis, and it represents the range or values of a variable in the horizontal direction. In a two-dimensional coordinate system, the horizontal axis is perpendicular to the vertical axis.

The coordinate system is often represented by a plane, called the Cartesian plane. The x-axis and y-axis divide the plane into four quadrants. The x-axis is usually marked with positive values to the right of the origin and negative values to the left. The y-axis is marked with positive values above the origin and negative values below.

The x-axis and y-axis together form a coordinate grid where points can be located using their x and y coordinates. The x-coordinate represents the position of a point along the horizontal axis, while the y-coordinate represents the position of a point along the vertical axis.

The axes are typically marked with a scale to indicate the intervals between values. The scale helps in measuring distances and determining the position of points accurately. The interval between values on the x-axis and y-axis can be different, depending on the context of the graph or the data being represented.

Key Properties of the X-Axis

The x-axis is a fundamental concept in math and geometry, and it plays a central role in understanding coordinate systems and graphs. Here are some key properties of the x-axis:

• Definition: The x-axis is a horizontal line on a coordinate plane. It is usually depicted as a straight line running from left to right. The x-axis represents the horizontal axis or the horizontal dimension of a two-dimensional space.
• Origin: The point where the x-axis intersects the y-axis is called the origin. It is denoted by the coordinates (0, 0). This point is important because it serves as the reference point for all other points on the coordinate plane.
• Direction: The x-axis extends infinitely in both positive and negative directions. The positive direction is to the right of the origin, while the negative direction is to the left of the origin.
• Variable: The x-axis represents the independent variable in a graph or equation. It is commonly used to represent time, distance, or any other variable that can change value.
• Number Line: The x-axis can be thought of as a number line, where each point on the line corresponds to a unique number. The numbers increase in value as you move to the right along the x-axis and decrease in value as you move to the left.
• Range: The x-axis covers a range of real numbers. The values on the x-axis can be positive, negative, or zero.
• Scale: The x-axis is typically marked with equally spaced tick marks or intervals to indicate the scale or units of measurement. The spacing between the tick marks represents equal intervals or increments.
• Line: The x-axis is represented as a straight line, parallel to the y-axis, with no curvature or bends.
• Graph: When plotting points on the coordinate plane, the x-coordinate represents the distance or position along the x-axis. The x-axis divides the plane into two equal halves: the positive x-axis and the negative x-axis.

Understanding the key properties of the x-axis is essential in many areas of math and geometry, as it provides a framework for analyzing and interpreting data, graphing functions, and solving equations.

Linearity and Directionality

Linearity refers to the property of the x-axis in mathematics that it is a straight line. It is always horizontal and extends infinitely in both positive and negative directions. The x-axis is one of the two coordinate axes in the Cartesian coordinate system, which is widely used in mathematics and physics.

The x-axis represents the scale of the horizontal variable in mathematical equations and functions. The origin is marked at the center of the x-axis, which represents the zero point. Any positive number on the x-axis represents a value greater than zero, while any negative number represents a value less than zero.

Directionality is an important concept associated with the x-axis. It determines the direction of values represented on the x-axis. As the x-axis extends from left to right, the positive values are located on the right side, while the negative values are located on the left side of the origin.

In geometry and graph theory, the x-axis is used to represent the interval of values for a specific range. It allows for the representation of mathematical functions and the plotting of data points. The x-axis is often labeled with numeric values that correspond to the specific value being represented.

The x-axis is an essential component of the Cartesian coordinate system, providing a visual representation of relationships between two variables. It enables accurate measurement and analysis of mathematical models, equations, and data points. The x-axis plays a vital role in various branches of mathematics and science, facilitating the study and understanding of complex concepts and phenomena.

Intersection with the Y-Axis

When we talk about the intersection of a graph or a line with the y-axis in math, we are referring to the point where it crosses or touches the vertical line that represents the y-coordinate. The y-axis is one of the two perpendicular lines used to create a coordinate plane, with the other being the x-axis. Together, they form the Cartesian coordinate system, which is widely used in algebra, geometry, and other areas of mathematics.

The y-axis is a horizontal line that extends from the origin – the point where the x-axis and y-axis intersect – in both positive and negative directions. The values on the y-axis represent the y-coordinates, which are often associated with the dependent variable in a mathematical equation or function.

When a graph or line intersects the y-axis, it means that the x-coordinate at that point is always 0. This occurs because the y-axis is a vertical line, and all points on that line have an x-coordinate of 0. Therefore, the intersection of a graph or line with the y-axis can be represented as the point (0, y), where y is the value of the y-coordinate at that intersection.

The intersection of a graph or line with the y-axis can also provide important information about the behavior of the function or equation. For example, the y-intercept – the point where a line intersects the y-axis – can indicate the initial value or starting point of a function. Additionally, the slope of the line can be determined by its intersection with the y-axis, as it represents the rate of change of the dependent variable with respect to the independent variable.

Graphing and Plotting

In mathematics, graphing and plotting are essential tools for visualizing mathematical functions and relationships. They allow us to understand and analyze data and patterns in a more tangible way.

A graph is a visual representation of data that shows the relationship between two or more variables. It consists of two axes, the x-axis and the y-axis, which are usually perpendicular to each other. The x-axis represents the independent variable, and the y-axis represents the dependent variable.

The x-axis is a horizontal line that extends infinitely in both positive and negative directions. It serves as a reference line for measuring the value of the variable plotted on it. The range of the x-axis depends on the specific problem or situation being represented.

The interval on the x-axis is the distance between consecutive points or values. It is usually divided into equal intervals to create a scale. The scale allows us to determine the value of a variable at a specific point on the x-axis.

In geometry, the x-axis is often referred to as the horizontal axis because it lies in a flat plane known as the Cartesian plane. The x-axis intersects the y-axis at a point called the origin, which has coordinates (0, 0). This point serves as the reference point for plotting data on the graph.

When graphing on the x-axis, positive numbers are plotted to the right of the origin, while negative numbers are plotted to the left. The x-axis allows us to represent a wide range of values, including whole numbers, fractions, decimals, and even irrational numbers.

Understanding the x-axis and its properties is crucial in math and various fields, such as physics, finance, and engineering. It enables us to analyze and interpret data more effectively, make predictions, and solve problems in real-life scenarios.

Applications and Examples

Applications and examples of the x-axis can be found in various fields of mathematics and beyond. Here are a few key examples:

• The x-axis is used in graphing to represent the horizontal line on a coordinate plane. This plane is often referred to as the Cartesian plane, which is commonly used in geometry and other areas of math.
• The x-axis is often used to represent a variable or independent variable in mathematical equations and functions. For example, in the equation y = mx + b, the x-axis represents the variable x and the corresponding values of y can be plotted on the y-axis.
• In geometry, the x-axis is used to determine the position of points in a 2-dimensional plane. The x-coordinate of a point represents its horizontal position relative to the origin, which is the point where the x-axis and the y-axis intersect.
• The x-axis is also used in creating scale and interval on graphs. For example, in a bar graph, the x-axis often represents different categories or groups, while the height of the bars represents the corresponding values or frequencies.
• In the context of negative and positive numbers, the x-axis allows us to represent negative values to the left of the origin and positive values to the right. This helps in visualizing and understanding the range of values in a given scenario.

Overall, the x-axis is a fundamental component of the Cartesian coordinate system and has numerous applications in math, graphing, geometry, and other fields where the representation of values and variables on a horizontal plane is required.

Coordinate Plane and Graphs

The coordinate plane is a two-dimensional system used in mathematics and geometry to represent points and lines. It consists of two perpendicular axes, the x-axis and the y-axis, which intersect at a point called the origin. The x-axis is a horizontal line, while the y-axis is a vertical line.

A graph is a visual representation of data or a mathematical equation in which points are plotted on the coordinate plane. The x-axis is typically used to represent the independent variable or the input, while the y-axis represents the dependent variable or the output. The values on the x-axis usually increase in a positive direction from left to right, and the values on the y-axis increase in a positive direction from bottom to top.

In Cartesian or rectangular coordinates, the x-axis represents the horizontal coordinate or the x-coordinate, while the y-axis represents the vertical coordinate or the y-coordinate. The coordinates of a point on the coordinate plane are written as (x, y), where x represents the distance from the origin along the x-axis and y represents the distance from the origin along the y-axis.

The x-axis and y-axis divide the coordinate plane into four quadrants: the first quadrant, second quadrant, third quadrant, and fourth quadrant. Each quadrant has its own set of positive and negative values for both the x-axis and y-axis.

The x-axis and y-axis can be thought of as number lines, with the x-axis representing a horizontal number line and the y-axis representing a vertical number line. The scale or interval between the numbers on each axis can be adjusted to represent different ranges of values. This allows for precise measurement and representation of data on the coordinate plane.

Equations and Functions

In mathematics, equations and functions are used to model relationships between variables. An equation is a mathematical statement that shows equality between two expressions, while a function is a rule that assigns each input value to exactly one output value.

Equations and functions are often represented graphically, using a coordinate plane. The coordinate plane consists of two perpendicular lines called axes: the x-axis and the y-axis. The x-axis is the horizontal line, and the y-axis is the vertical line. The point where the two axes intersect is called the origin, which is assigned the coordinates (0, 0).

The x-axis is used to represent the input values or independent variable in an equation or function. It is typically labeled with the variable name, such as x, and is divided into equally spaced intervals. The intervals on the x-axis are often represented by tick marks and a scale to indicate the value of each interval.

The x-axis extends in both positive and negative directions. The positive direction is to the right of the origin, while the negative direction is to the left. The values on the x-axis increase in magnitude as you move further away from the origin in either direction.

Equations and functions can be represented as graphs on the coordinate plane. The graph of an equation or function is a visual representation of all the points that satisfy the equation or function. On the graph, the x-axis represents the possible input values, while the y-axis represents the corresponding output values or dependent variable.

In geometry, the x-axis is an essential component for representing geometric figures and measurements. It helps determine the position, direction, and length of various geometric elements. For example, the length of a line segment can be measured by comparing the x-coordinates of its endpoints on the x-axis, considering the direction from left to right.

In summary, the x-axis in mathematics is a horizontal line on a coordinate plane used to represent the input values of equations and functions. It has positive and negative directions, an origin at (0, 0), and scales to indicate the magnitude of values on the axis. Understanding the x-axis is crucial for analyzing equations, functions, and geometric figures in various math-related fields.

Real-World Representations

In real-world scenarios, the x-axis is often used to represent a scale or measurement. For example, in a plane or map, the x-axis can represent the horizontal direction, while the y-axis represents the vertical direction. This allows us to determine the coordinates of a point using two variables: the x-coordinate and the y-coordinate.

In math and geometry, the x-axis is typically represented as a horizontal line that intersects the y-axis at the origin. The positive direction of the x-axis extends to the right, while the negative direction extends to the left. The x-axis divides the Cartesian plane into two halves: the positive x-axis and the negative x-axis.

The x-axis also determines the range of values that can be plotted on a graph. For example, if we have a graph that represents time on the x-axis and temperature on the y-axis, the x-axis would show the intervals of time, such as minutes, hours, or days. This allows us to see how the temperature changes over a specific time interval.

By using the x-axis as a reference, we can locate points on a coordinate plane and understand their positions in relation to other points or objects. The x-axis provides an essential framework for understanding graphs, equations, and relationships between variables in various mathematical and scientific fields.